numpy Matrix for linear algebra
Hello readers, I welcome you to this second part of the tutorial series where I talk about the next important topic numpy matrix .
First of let me share the the different items that we are going to cover here in this page. As our focus is matrix using the numpy library, I shall divide the topic in below sections.
- First I shall share an Introduction
- Then I shall talk about the different matrix operations using numpy
- Finally I shall show how we can access the values from a matrix
Introduction
What is a matrix ?
Firstly a matrix is a data structure to store value in a row/column manner. And here if the collection contains “m” rows and “n” columns, then we say that the size of the matrix is m*n
Therefore if you take a look at the below image you will see that the matrix contains total 4 elements ( 2 rows and 2 columns ) . Thus the size is 2*2 = 4
Next what are the i and j doing here ?
Well to answer to that, i and j are simple the index to access the row and column positions respectively
And just to make things clear, the R represents real number

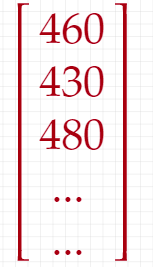
What is a vector then ?
To answer the question, it is sufficient to just mention that a vector has just one column. Therefore the size of any vector is always m*1
What is a Python matrix ?
Well there is no data-type in python named matrix, but we can represent a matrix using list.
And here is how a matrix is represented in python
Original matrix

Python version of the original matrix
Here we are representing each row with a List data type.

Why we need numpy if python list can represent a matrix ?
Well this is a very good point, and the simple answer would be “it’s complicated”.
As working with List data-type may appear easy for simple and smaller dimension matrix. But as soon as the dimension grows or the size of the matrix grows, using List also becomes complicated. And that’s why there is numpy for rescue.Check here for more details
How to create a matrix using numpy ?
First I need to mention that numpy leaverages a function called array() for both vector and matrix,
Let’s create a vector with numpy
import numpy as np a = np.array([1, 2, 3]) print(a) # Output: [1, 2, 3] print(type(a)) # Output: <class 'numpy.ndarray'>
And you spotted the ndarray precisely. The datatype from numpy is ndarray
Let’s create a matrix with numpy
Well as might have already guessed, the same array() function can be used for matrix too. Here is how it is done .
import numpy as np A = np.array([[1, 2, 3], [ 4, 5, 6]]) print(A)
More on numpy array
Let’s see a few more utilities of the numpy array() function.
I shall show how we can create arrays with different data types ( for example -> float type , as float type array is used vastly in machine learning applications), and also ways to create array of zeros and ones
create np array with float type
import numpy as np A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Array of floats print(A)
Output of the above would be
[[1.1 2. 3. ]
[3. 4. 5. ]]
create np array with complex type
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Array of complex numbers print(A)
Output of the above would be
[[1.+0.j 2.+0.j 3.+0.j]
[3.+0.j 4.+0.j 5.+0.j]]
Array of zeros and ones:
import numpy as np zeors_array = np.zeros( (2,4) ) print(zeors_array) ''' Output: [[0. 0. 0.] [0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (2, 3), dtype=np.int32 ) // specifying dtype print(ones_array) # Output: [[1 1 1 1 1 1]]
Using arange() and shape()
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Output:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
matrix operations
First to talk about operations, I want to mention the ones that are going to be very useful.
And the most common ones are
- Addition
- Multiplication
- Transpose
Addition
Multiplication
Element wise multiplication
Let’s first see how the element wise multiplication works. And for this we will be using multiply() function from numpy library
import numpy as np
arr1 = np.array([[1, 2],
[3, 4]])
arr2 = np.array([[5, 6],
[7, 8]])
arr_result = np.multiply(arr1, arr2)
print(arr_result)
If you have guessed already, the result will be like this,
[[ 5 12]
[21 32]]
matrix multiplication using
matmul()function
First take a look at the below diagram that shows how the multiplication is performed
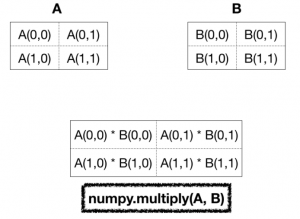
Here you see how the multiplication is done actually.
Now take an example and illustrate how the multiplication would look like. For this let’s assume that we the below two matrices.
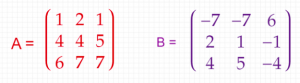
Now from the illustration you may be already guessing how the values would be for each position !
Here is how they would look like

So now you may be getting the final result of the multiplication :
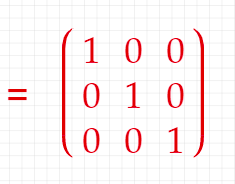
do you notice something ? Like a pattern . Actually the result is called and identity matrix and the two matrices A and B are called Inverse matrix.
Let’s see how can we code the above example
import numpy as np
arr1 = np.array([[1, 2, 1],
[4, 4, 5],
[6, 7, 7]])
arr2 = np.array([[-7, -7, 6],
[2, 1, -1],
[4, 5, -4]])
arr_result = np.matmul(arr1, arr2)
print(f'Matrix Product of arr1 and arr2 is:\n{arr_result}')
Transpose
Now let’s focus on what a transpose matrix is !
Let’s consider that we have the below metrix.
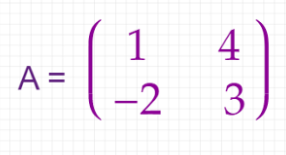
Now if we apply the transpose() function from the numpy library, then the matrix will become like this
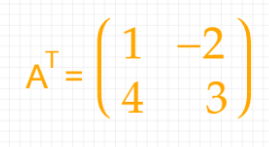
So let’s see how can we code the same
import numpy as np A = np.array([[1, 4], [-2, 3]]) print(A.transpose()) ''' Output: [[ 1 -2] [ 4 3]] '''
Access the values from a matrix
elements
Simillarly, just like in the case of python lists, we can access matrix elements using index. Let’s start with a one-dimensional NumPy array.
import numpy as np
A = np.array([1, 2, 3, 4, 5])
print("A[0] =", A[0]) # First element
print("A[2] =", A[2]) # Third element
print("A[-1] =", A[-1]) # Last element
Now if I run this code, it will give an output like this
A[0] = 1
A[2] = 3
A[-1] = 5
Now let’s see how we can access values from a 2-dimensional array
2D array
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# First element of first row
print("A[0][0] =", A[0][0])
# Third element of second row
print("A[1][2] =", A[1][2])
# Last element of last row
print("A[-1][-1] =", A[-1][-1])
And we run the program, the output will be:
A[0][0] = 1
A[1][2] = 9
A[-1][-1] = 19
Access rows of a Matrix
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # First Row
print("A[2] =", A[2]) # Third Row
print("A[-1] =", A[-1]) # Last Row (3rd row in this case)
When we run the program, the output will be:
A[0] = [1, 4, 5, 12]
A[2] = [-6, 7, 11, 19]
A[-1] = [-6, 7, 11, 19]
Access columns of a Matrix
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # First Column
print("A[:,3] =", A[:,3]) # Fourth Column
print("A[:,-1] =", A[:,-1]) # Last Column (4th column in this case)
When we run the program, the output will be:
A[:,0] = [ 1 -5 -6]
A[:,3] = [12 0 19]
A[:,-1] = [12 0 19]
If you don’t know how this above code works, read slicing of a matrix section of this article.
Slicing of a Matrix
Slicing of a one-dimensional NumPy array is similar to a list. If you don’t know how slicing for a list works, visit Understanding Python’s slice notation.
Let’s take an example:
import numpy as np
letters = np.array([1, 3, 5, 7, 9, 7, 5])
# 3rd to 5th elements
print(letters[2:5]) # Output: [5, 7, 9]
# 1st to 4th elements
print(letters[:-5]) # Output: [1, 3]
# 6th to last elements
print(letters[5:]) # Output:[7, 5]
# 1st to last elements
print(letters[:]) # Output:[1, 3, 5, 7, 9, 7, 5]
# reversing a list
print(letters[::-1]) # Output:[5, 7, 9, 7, 5, 3, 1]
[/pyhton]
Now, let's see how we can slice a matrix.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # two rows, four columns ''' Output: [[ 1 4 5 12] [-5 8 9 0]] '''
print(A[:1,]) # first row, all columns ''' Output: [[ 1 4 5 12 14]] '''
print(A[:,2]) # all rows, second column ''' Output: [ 5 9 11] '''
print(A[:, 2:5]) # all rows, third to the fifth column '''Output: [[ 5 12 14] [ 9 0 17] [11 19 21]] '''
As you can see, using NumPy (instead of nested lists) makes it a lot easier to work with matrices, and we haven’t even scratched the basics. We suggest you to explore NumPy package in detail especially if you trying to use Python for data science/analytics.